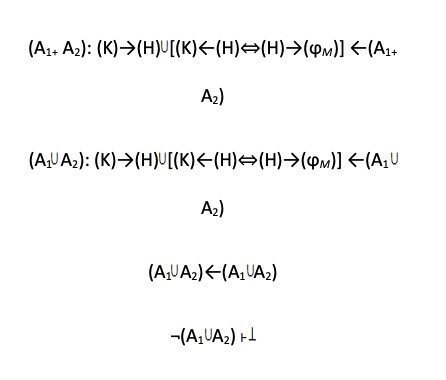Elements of Mathematical Logic for Consistency Analysis of Axiomatic Sets in the Mind-Body Problem
(...) However, whether we chose a weak or strong approximation, the set would not make any sense at all, if (once more) this choice would not be justified in either temporal or spatial sense or given the context of possible applicability of the set in different circumstances. This would obviously represent a dualism in itself as we would (for instance) posit and apply a full identity-equality-equivalence of x and y when applying Newtonian physics to certain observations we make (it would be the case of neural correlates), and we would posit and apply a non - identity-equality-equivalence of x and y when applying Quantum mechanics to other observations. Following this dualism in and of theories, the same sate would need to be slightly modified: U2:(x~y)∪(x≈y); U3:(x~y)∩(x≈y); U4a:(x~y)⊆(x≈y) vs. U4b:(x~y)⊇(x≈y)